华为麒麟芯片最新动态

如何从麦克斯韦方程组解出毕奥萨伐尔定律？

毕奥萨伐尔定律是描述电流在一定距离外引起磁场的规律，它是电磁学的基本定律之一，在电工学、电子学、物理学等领域有广泛应用。本文将介绍如何从麦克斯韦方程组解出毕奥萨伐尔定律，并对其进行详细解释。

麦克斯韦方程组包含四个方程：

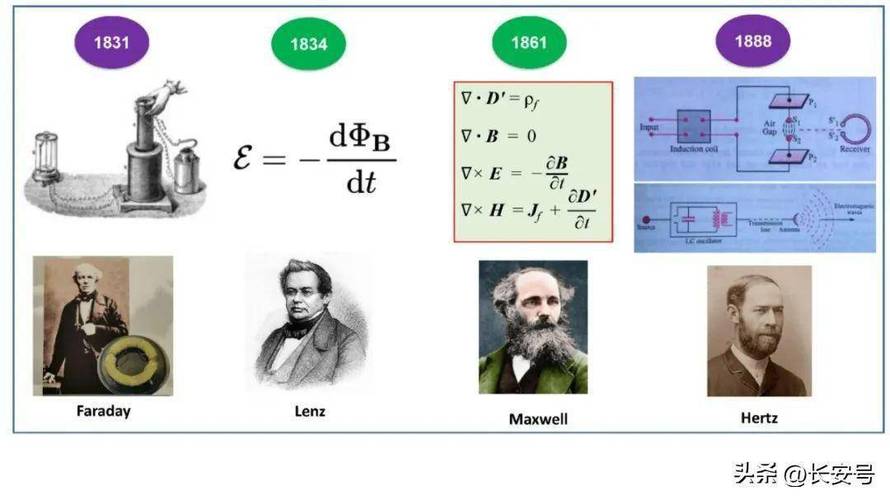
1. 静电场高斯定理：$\mathrm{\nabla\cdot E}=\frac{\rho}{\epsilon}$

2. 静磁场高斯定理：$\mathrm{\nabla\cdot B}=0$

3. 法拉第电磁感应定律：$\mathrm{\nabla\times E}=\frac{\partial B}{\partial t}$

4. 安培环路定理：$\mathrm{\nabla\times B}=\mu_0\left(\mathrm{J} \epsilon_0\frac{\partial E}{\partial t}\right)$

其中，$\mathrm{E}$ 和 $\mathrm{B}$ 分别代表电场和磁场，$\rho$ 为电荷密度，$\mathrm{J}$ 为电流密度，$\epsilon$ 为介电常数，$\mu_0$ 为真空磁导率，$\epsilon_0$ 为真空介电常数。

根据法拉第电磁感应定律，我们可以推导出电场的旋度：

$$\mathrm{\nabla\times E}=\frac{\partial B}{\partial t}$$

根据矢量恒等式，我们可以将旋度和散度互相转化：

$$\mathrm{\nabla\times(\nabla\times E)}=\mathrm{\nabla(\nabla\cdot E)}\mathrm{\nabla^2E}$$

代入静电场高斯定理，有：

$$\mathrm{\nabla\times(\nabla\times E)}=\mathrm{\nabla^2E}$$

再根据安培环路定理，我们可以推导出磁场的旋度：

$$\mathrm{\nabla\times B}=\mu_0\mathrm{J}$$

代入静磁场高斯定理，有：

$$\mathrm{\nabla\cdot B}=0$$

将上述两个方程代入矢量恒等式中，有：

$$\mathrm{\nabla\times(\nabla\times B)}=\mathrm{\nabla^2B} \mathrm{\nabla(\nabla\cdot B)}=\mathrm{\nabla^2B}$$

综合以上几个公式，可以得到磁场的波动方程：

$$\mathrm{\nabla^2B}=\mu_0\mathrm{J} \mu_0\epsilon_0\frac{\partial^2 B}{\partial t^2}$$

上式说明，磁场是一种横波，它在介质中传播的速度为：$\mathrm{v}=\frac{1}{\sqrt{\mu_0\epsilon_0}}=\mathrm{c}$，即磁场的速度等于光速。

在真空中，上述方程简化为：

$$\mathrm{\nabla^2B}=\mu_0\epsilon_0\frac{\partial^2 B}{\partial t^2}$$

对于一个定向的电流，我们可以将其表示为一个电流元，即：

$$\mathrm{dI=JdS}$$

其中，$\mathrm{S}$ 为电流元的截面积。根据毕奥萨伐尔定律，电流元产生的磁场$\mathrm{dB}$ 的磁感应强度为：

$$\mathrm{dB}=\frac{\mu_0}{4\pi}\frac{\mathrm{dI}\times\mathrm{r}}{r^3}$$

其中，$\mathrm{r}$ 为距离电流元的位置，$\times$ 为叉乘运算符。

将电流元表示为电流密度的积分形式：

$$\mathrm{I}=\int\mathrm{JdS}$$

代入毕奥萨伐尔定律，我们可以计算电流在某一点产生的磁场，即：

$$\mathrm{B}=\frac{\mu_0}{4\pi}\int\frac{\mathrm{J}\times\mathrm{r}}{r^3}\mathrm{dS}$$

这就是毕奥萨伐尔定律的数学表达式。

从麦克斯韦方程组解出毕奥萨伐尔定律的过程比较繁琐，但只要熟练掌握基本的电磁学知识，就可以轻松理解。在实际应用中，我们可以利用毕奥萨伐尔定律计算电流在某一点产生的磁场，帮助我们解决各种实际问题。

附：磁矢势

磁矢势是电磁场中的一个重要概念，它是描述磁场的一个向量场。在洛伦兹力的公式中，磁场的作用只与它的旋度有关，与散度无关，因此，我们可以定义一个向量场 $\mathrm{A}$，使得：

$$\mathrm{B}=\mathrm{\nabla\times A}$$

其中，$\mathrm{B}$ 为磁场强度。磁矢势具有一定的数学性质，可以简化计算，特别是在处理电磁波传播问题时，磁矢势有着重要的应用价值。