张朝阳的物理课理想气体状态方程与麦克斯韦速度分布律的奥秘

在物理学的广阔天地中，理想气体状态方程与麦克斯韦速度分布律是两个极为重要的概念，它们不仅在理论物理中占据核心地位，也在实际应用中发挥着巨大作用。本文将深入探讨这两个概念，并展示如何在《张朝阳的物理课》中巧妙地将它们结合起来，揭示气体分子运动的深层规律。

理想气体状态方程：PVT的和谐统一

理想气体状态方程，即PV=nRT，是描述理想气体在平衡状态下压力P、体积V和温度T之间关系的方程。其中，n是气体的摩尔数，R是理想气体常数。这个方程简洁而深刻，它不仅反映了宏观物理量之间的关系，也隐含了微观粒子的行为。

在《张朝阳的物理课》中，张朝阳老师通过生动的实验和直观的图示，向学生们展示了如何从微观粒子的碰撞出发，推导出理想气体状态方程。他强调，理想气体模型假设气体分子之间没有相互作用力，分子本身不占有体积，这些简化使得方程更加易于理解和应用。

麦克斯韦速度分布律：速度的舞蹈

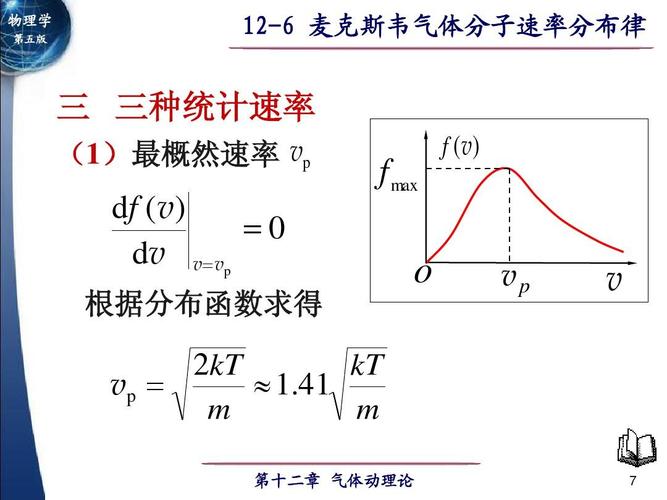
麦克斯韦速度分布律描述了在一定温度下，理想气体分子速度的概率分布。这个分布律揭示了气体分子速度的统计规律，即速度的分布呈现出一种特定的形态，其峰值对应的是最可能的速度，而速度的平均值和方均根值则提供了速度分布的中心和扩散程度的信息。

在《张朝阳的物理课》中，张朝阳老师通过数学推导，向学生们展示了如何从基本的统计力学原理出发，得到麦克斯韦速度分布律。他解释了分布律中的指数因子如何反映了分子动能与温度之间的关系，以及如何通过分布律预测不同温度下气体分子的平均动能。

结合与推导：微观与宏观的桥梁

在《张朝阳的物理课》中，最精彩的部分莫过于将理想气体状态方程与麦克斯韦速度分布律结合起来，推导出气体分子速度分布的完整图景。张朝阳老师首先从理想气体状态方程出发，引入了分子动能的概念，然后利用统计力学的方法，推导出速度分布律。

他详细解释了如何通过玻尔兹曼常数将微观粒子的动能与宏观的温度联系起来，以及如何利用速度分布律计算气体分子的平均自由程和碰撞频率。这一过程不仅加深了学生对理想气体模型的理解，也让他们领略了统计物理学的魅力。

结论：物理学的魅力与应用

通过《张朝阳的物理课》，学生们不仅学到了理想气体状态方程和麦克斯韦速度分布律的理论知识，更重要的是，他们学会了如何将这些理论应用于解决实际问题。无论是预测气体在不同条件下的行为，还是设计高效的气体动力系统，这些知识都显示了物理学在现代科技中的重要作用。

《张朝阳的物理课》不仅是一堂精彩的物理课，更是一次探索自然规律、启迪思维的旅程。通过结合理想气体状态方程与麦克斯韦速度分布律，张朝阳老师向我们展示了物理学的深刻与美丽，激发了我们对科学探索的热情。