深入解析应力张量从基础概念到纳维-斯托克斯方程的推导

在物理学和工程学中，应力张量是一个关键的概念，它描述了物体内部各点在不同方向上的力分布情况。在《张朝阳的物理课》中，应力张量的概念被深入探讨，并用于推导流体力学中的纳维斯托克斯方程。本文将详细解释应力张量的含义，并概述如何通过应力张量来推导纳维斯托克斯方程。

1. 应力张量的基本概念

应力张量是一个二阶张量，通常用符号 $\sigma$ 表示。在三维空间中，它由9个分量组成，可以表示为一个3x3的矩阵。这些分量描述了物体内部任意一点在三个正交方向上的应力状态。应力张量的每个分量 $\sigma_{ij}$ 表示在垂直于 $i$ 方向的面上沿 $j$ 方向的应力。

应力张量可以分为两个部分：正应力和剪应力。正应力是垂直于作用面的应力，而剪应力则是平行于作用面的应力。在连续介质力学中，应力张量是对称的，即 $\sigma_{ij} = \sigma_{ji}$，这意味着只有6个独立的分量需要考虑。

2. 应力张量与流体动力学

在流体动力学中，应力张量特别重要，因为它描述了流体内部的压力和粘性力。对于理想流体（无粘性），应力张量简化为各向同性的压力项。然而，对于实际流体，如水和空气，粘性效应必须考虑，这导致应力张量包含额外的剪应力项。

3. 推导纳维斯托克斯方程

纳维斯托克斯方程是描述流体运动的偏微分方程，它基于牛顿第二定律，将流体的加速度与作用在流体上的力联系起来。在《张朝阳的物理课》中，通过考虑流体微元上的力平衡，可以推导出纳维斯托克斯方程。

考虑一个流体微元，其体积为 $\Delta V$，表面为 $\Delta S$。作用在这个微元上的力包括体积力和表面力。体积力（如重力）可以直接计算，而表面力则由应力张量描述。通过将这些力与微元的加速度联系起来，可以得到纳维斯托克斯方程：

$$

\rho \left( \frac{\partial \mathbf{v}}{\partial t} (\mathbf{v} \cdot \nabla) \mathbf{v} \right) = \nabla p \nabla \cdot \boldsymbol{\sigma} \rho \mathbf{g}

$$

其中，$\rho$ 是流体密度，$\mathbf{v}$ 是流体速度，$p$ 是压力，$\boldsymbol{\sigma}$ 是应力张量，$\mathbf{g}$ 是体积力（如重力）。

4. 应力张量的物理意义

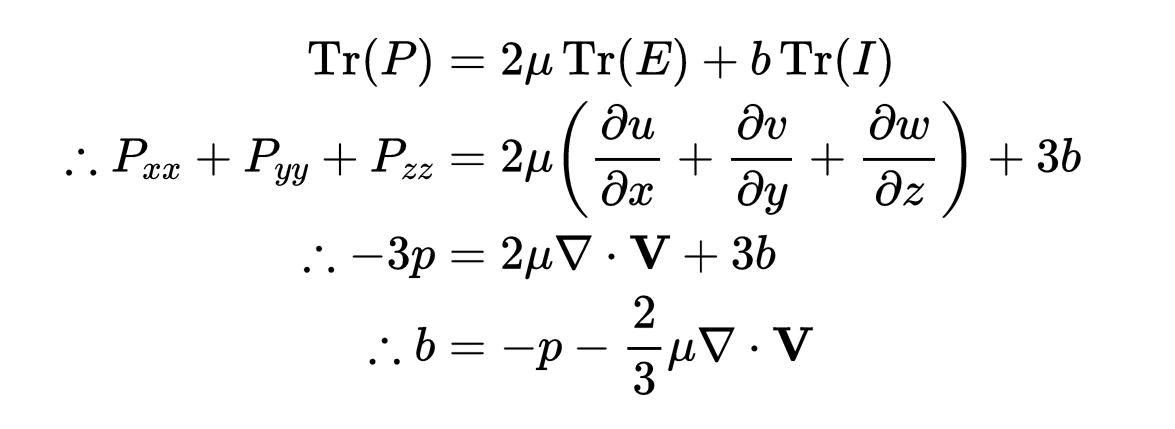
应力张量的物理意义在于它提供了流体内部力分布的完整描述。通过分析应力张量的各个分量，可以了解流体在不同条件下的行为，如流动稳定性、湍流产生等。

5. 结论

应力张量是理解和分析流体动力学的关键工具。通过《张朝阳的物理课》中的深入讲解和推导，我们不仅理解了应力张量的基本概念，还学会了如何将其应用于推导纳维斯托克斯方程。这些知识对于工程设计、天气预报、海洋学等领域都具有重要的实际意义。

通过这篇文章，我们希望读者能够对应力张量及其在流体动力学中的应用有一个清晰的理解，并能够欣赏到物理学在解决实际问题中的强大力量。